
Prompt Images
Global warming. Nuclear annihilation. Robotic uprisings. These are all worrisome things. They are things I think about now and then during the day, when my mind is inundated by a flash flood of news and memes. But these are not the things that keep me up at night.
What keeps my mind turning late at night is a problem that is much older than those listed above.
It’s a problem that goes back to 1742. That’s when Christian Goldbach proposed what is now known as Goldbach’s conjecture:
Every even number greater than 2 can be written as the sum of two prime numbers.
If Goldbach’s conjecture is true, it means that you can pick any even number N, and I should be able to find two prime numbers that add up to N. We know this is true for many, many numbers. Obviously, 4 (an even number) = 2 + 2 (both prime.) Ditto for 6 = 3 + 3. 8 = 5 + 3. Mathematicians have checked that this works all the way up to 4 × 1018. But since there is an infinite number of numbers, you can’t prove this conjecture by checking every possibility. You need a general proof that works for arbitrary N.
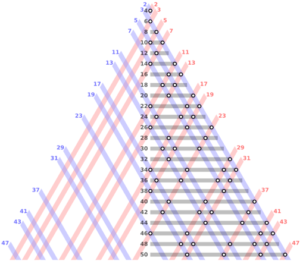
This pretty picture shows the primes running down the two sides of the triangle. The intersections of the blue and red lines give a particular even number. Note that some even numbers (like 16) have more than one decomposition into a sum of primes.
All the evidence seems to suggest the conjecture is true. But no one knows how to prove it.
And that, my friends, is what keeps me up at night. A math problem.

But give me a chance to explain myself. It isn’t the substance of the conjecture that I care so much about. Whether or not the conjecture is true or false is sort of irrelevant to anyone not publishing regularly in the Bulletin of Math Dorks. What keeps me up at night is the implicit meta problem:
How have we gone almost three centuries without solving a math problem that I could explain to an intelligent four-year-old?
If you aren’t convinced that this is kind of crazy, consider the situation from the perspective of someone living in the world in 1742 when old Christian laid down this mathematical gem. Suppose we were to give a survey to the average person living in 1742 with the following question:
Which of the following do you think is least likely to happen at some point during the next 300 years?
A. A person walking on the moon.
B. The discovery of atoms.
C. Humans creating a weapon so powerful it can level a city in less than a second.
D. Someone proving/disproving that every even number greater than 2 can be written as the sum of 2 primes.
E. The continued existence of a Flat Earth Society.
Clearly, a lot of these options would seem almost comically impossible to someone in 1742. Getting to the moon? Observing atoms? Leveling a city in a second? A flat earth society – didn’t Columbus settle that one in 1492? But one thing we can be absolutely sure of is that nobody from 1742 is looking at this list and circling (D), the option about a math problem so simple that even Joseph the Blacksmith can understand it. (D) is like one of those answers that test makers always seem to throw in: an answer that is weirdly specific and wildly unrealistic which you can immediately toss out to improve your odds of getting the right answer.
And yet (D) stands alone as the one thing on this list that hasn’t yet happened. What’s worse, there’s no reason to believe it’s something we will have solved within another 300 years.
I shudder to think of a future when we are all digital gods beaming ourselves around the universe, discovering new dimensions of space and consciousness that would be unfathomable to our current selves, but also, we’ve failed to prove that every even integer can be written as the sum of two primes.
Beyond Pythagoras
Goldbach’s conjecture is part of a branch of mathematics known as number theory. And while it may be one of the most famous open problems in this area, Goldbach’s conjecture is actually quite representative of many, many problems in number theory: problems that are easy to state and fiendishly difficult to prove.
Consider Fermat’s Last Theorem about a generalization of the Pythagorean Theorem. In high school we are taught that the lengths of the three sides of a triangle are related by the following algebraic equation:
a2+ b2= c2
We all remember our Pythagorean triples, right? Those sets of three integers that satisfy this equation and, thus, provide examples of right triangles with sides of integer length? 3, 4, 5? 5, 12, 13? Anyone?
Well, in the 1630’s, 100 years or so before Goldbach came up with his conjecture on the sums of primes, Pierre de Fermat made a conjecture about the Pythagorean equation for other powers. He conjectured the following:
For the general equation an+ bn= cn, you can’t find (non-zero) integer solutions for (a,b,c) when n is greater than 2.
A specific example would be the case n = 3. In that case, the conjecture implies that the equation a3+ b3= c3 has no solutions where a, b, c are all non-zero integers. (Go ahead and try every possible set of integer combinations from 1, 1, 1 to ∞, ∞, ∞ if you don’t believe me. I’ll wait.)
Again, here’s a reasonably simple problem to state; maybe a little more complicated than Goldbach’s conjecture, but still requiring only a basic understanding of algebra.
Unlike Goldbach’s conjecture, though, Fermat’s was solved … about 350 years after Fermat proposed it. The final proof came from Andrew Wiles, a mathematician at Princeton who had first discovered Fermat’s problem in a library book when he was 10.
Why did it take 350 years to solve this problem?
Perhaps the first few sentences from the introductory section of Andrew Wiles’ paper proving the theorem will provide some insight:
An elliptic curve over Q is said to be modular if it has a finite covering by a modular curve of the form X0(N). Any such elliptic curve has the property that its Hasse-Weil zeta function has …

The takeaway from this mumbo-math-jumbo is that while Fermat’s conjecture can be simply stated, the proof rests on some uber sophisticated mathematical constructs, many of which were only developed in the decades leading up to Wiles’ proof. BTW, the paper is about 200 pages long, and the above paragraph is basically casual banter compared to the many Lemmas and Theorems that follow.
OK, so a simple problem doesn’t imply a simple answer. But why did Fermat’s conjecture finally succumb to proof, while Goldbach’s remains in limbo?
Addition Is the Worst
Primes are really, really tough to work with. There’s no simple function that spits out the primes as there often is for other interesting sequences of numbers. They are defined in this strange, backwards-looking way: as a number that can’t be divided by any other integer that came before it (except 1, of course.)
The result of this awkward rule for generating primes is that, perhaps unsurprisingly, they are rather messy to work with. Their behavior is much closer to a random sequence than you’d intuitively expect. There’s very little structure to exploit, which is the whole point of mathematics – exploiting logical structure to prove things.
Of course, there are still lots of things people can prove about primes: that there is an infinite number of them or that every integer can be factored into a unique set of primes (e.g., 20 = 2 * 2 * 5.)
But Goldbach’s conjecture is really hard for another reason, too: that damn “+” sign. That “+” sign is the cause of so many troubles in number theory.
To understand why, we have to think about what addition and multiplication mean.
Multiplication is “repeated addition.” 3 * 3 = add 3 together 3 times: 3 + 3 + 3.
Because you are repeatedly doing something, multiplication generates a certain kind of pattern or symmetry. Patterns are what mathematicians can exploit when they want to prove something. For example, you can picture 3 * 3 as taking 3 rows of 3 blocks and stacking them atop each other to yield a square with 9 blocks. There’s some structure there we can work with! But now try adding 2, which gives you 11, and you no longer have a nice symmetric pile of blocks. You just have 11 blocks that you can arrange into various asymmetric piles.
Consider also that the patterns from multiplication are unique. You can only get 9 by multiplying 3 * 3 (or 9 * 1.) By contrast, with addition you can get 9 by 1 + 8, 2 + 7, 3 + 6, etc … There’s nothing special about breaking down 9 into 2 particular numbers with addition. There are a bunch of pairs of numbers that sum to 9. And when you have too many options, it can start to feel like those options are kind of meaningless.
And this is why Goldbach’s conjecture is so difficult.
Prime numbers have very little structure to exploit from the start, and the addition sign does little to add interesting structure to an equation. On the other hand, Fermat’s conjecture at least has some multiplication to leverage.
If trying to solve Fermat’s conjecture is like trying to climb a steep cliff with sharp jutting rocks that must be perfectly negotiated, Goldbach’s conjecture is a completely vertical slab with nothing but a few minor dents to grasp – a place where even these absurd goats would struggle to get a foothold.

Primes, Primes, Primes Everywhere
I know there are other “unsolvable problems” I could be worrying about at night. Poverty, structural racism, the role of Lance Stephenson on the new LeBron Lakers. But what’s different about these “real world” problems is that we knew from the start they’d be impossible to completely solve. The real world is messy and complicated, and the rules aren’t completely known to us (doubly so in the case of Lance Stephenson.) By contrast, mathematics is a highly controlled environment where we not only know most of the rules, but we actually created them.
It’s a game we’ve been playing for thousands of years – a game that we, as a species, are really good at.
But Goldbach’s conjecture, and the myriad of other problems that are simple to state but nearly impossible to solve, stands out as a hole in our understanding of the game. They are a constant reminder of how little we actually know.
So during the day, I’ll scroll through my social media feeds and bemoan the state of the world and the impending collapse of the liberal order. But at night? At night, you will find me laying in bed, quietly cursing Christian Goldbach under my breath for pulling a conjecture out of his ass and leaving the mathematical world with not so much a problem but a paradox: how can the species that invented prime numbers and addition be so clueless about how these things work?
