Part II: Torn Asunder

In Part I, I talked about how some physicists have been going around saying that spacetime is doomed. In Part II we are going to see how these physicists are currently working to demolish spacetime as we know it.

Juan and the Holograms

Let’s take one step back from talking about the emergence of spacetime itself and consider the emergence of gravity. Gravity is special because it is intimately related to spacetime. Einstein taught us to think about gravity as a curvature in spacetime, rather than as a force field that pervades spacetime (as appears to be the case for the other forces of nature).

So thinking about how gravity might be emergent is at least tangentially related to the idea of how spacetime might be emergent.

In 1997, the string theorist Juan Maldacena published a paper titled The Large N Limit of Superconformal Field Theories and Supergravity. Buried in a litany of technical details was a very provocative idea that has been at the center of much of the research on quantum gravity for two decades now. In his paper, Maldacena demonstrated that there was a direct correspondence between a theory of particles interacting via non-gravitational forces and a theory of strings interacting via gravity. More specifically, the theory including non-gravitational forces lives in a spacetime with D spatial dimensions (e.g., 2 spatial dimensions), while the theory using gravity lives in a spacetime with D+1 spatial dimensions (e.g., 3 spatial dimensions).

Say what now?

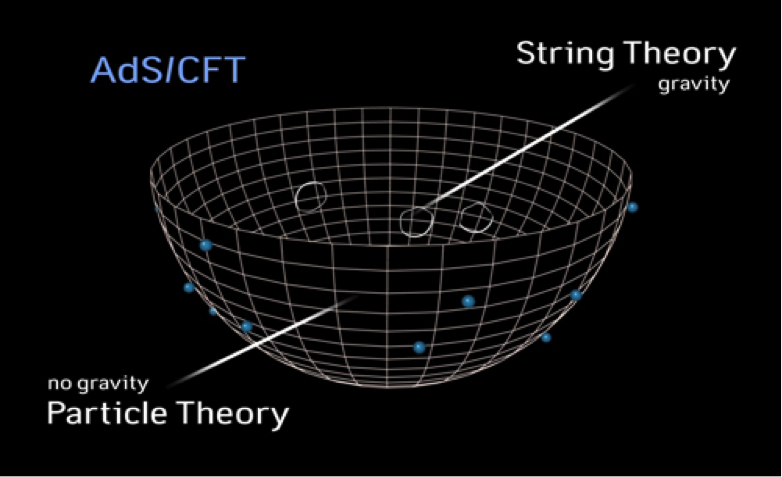
A Tale of Two Theories: Theory A — which has only particles and no gravity — lives on the 2D surface of a 3D space. Theory B — which has strings and gravity — lives in the 3D space. AdS/CFT implies these two theories are basically describing “the same thing.” Though the definitions of “same” and “thing” is now highly suspect…

Here’s a less technical explanation. Imagine Physicist A comes to you with a theory (Theory A) of physics that includes a bunch of forces (like electromagnetism) but not gravity. You are like, Cool beans. I don’t understand the math, but it seems reasonable.

Then Physicist B comes to you with a theory (Theory B) of physics that only includes strings and gravity. And also, they explain, Theory B lives in a spacetime with one more spatial dimension than Theory A (e.g., 3 dimensions instead of 2). Again, you think, Cool beans, though I feel I should point out that you dopes are using a different number of dimensions, which seems inconsistent with my experience that there are definitely a fixed number of dimensions.

Then physicist C comes along, studies Theory A and Theory B, and is like, Ohhhh snap! Same theory!

And you are like, Hold up—same theory? Theory A has no gravity, Theory B has only gravity. And they have a different number of dimensions!!!! How can they be “the same theory”?!?!

Physicist C writes down some fancy ass math and then shows that every interaction between particles in Theory A corresponds (in some well defined way) to an interaction between strings in Theory B, and vice versa.

If there is a problem to be solved in one theory, you can use Physicist C’s fancy math to translate the problem from one theory to the other. As a bonus, Physicist C shows how some problems in Theory A are easier to solve if you actually translate the problem to Theory B and solve it there.

Physicist C is Juan Maldacena.

And his observation that certain theories with non-gravitational forces have a direct correspondence with certain theories that have gravity is known as the AdS/CFT correspondence. Not to get too acronym-y on you, but AdS/CFT is a BFD in physics.

The paper where he introduced this idea, the one with that absurdly technical title? It’s the most cited paper in theoretical physics ever.

AdS/CFT stands for Anti-deSitter / Conformal Field Theory. To understand what those words mean, go get a Ph.D., in string theory. For our purposes, it just means a “correspondence” between two different kinds of physics theories in different kinds of spacetimes that is wholly surprising and, possibly, quite useful for practical calculations.

What does AdS/CFT imply about the universe, in an intuitive sense? Some folks like to claim it means our universe is a hologram. Recall that a hologram is a 3D image generated from 2D pictures. By analogy, a 4D universe (3 spatial dimensions + 1 time dimension) can be generated, using the AdS/CFT correspondence, from a 3D universe (2 spatial dimensions + 1 time dimension), albeit using different forces/particles.

The problem with this interpretation is that, as amazing as the AdS/CFT correspondence is, it’s not actually about our universe. It’s a correspondence between two kinds of mathematical worlds that don’t really look the universe we live in. Physicists have spent the last couple decades working towards something like the AdS/CFT correspondence that works for our actual universe, but so far, no dice.

Still, despite the mismatch between the hypothetical worlds of AdS/CFT and our actual universe, physicists can’t get over how suggestive AdS/CFT is: that the effects of gravity in one spacetime can be encoded in the non-gravitational interactions of particles in a lower dimensional spacetime. It suggests that gravity may not be not fundamental, because we can imagine doing physics in a theory that makes no reference to it.

The AdS/CFT correspondence is really, really cool. But it’s also about 20 years old now. And, as I’ve stated, it isn’t itself an attempt to explain how space and time emerge, but rather its about how gravity might be related to, or be encoded by, other kinds of physical interactions.

But it turns out that the AdS/CFT correspondence is useful in trying to understand how spacetime might be emergent. In fact, we are about to see how you can leverage AdS/CFT, along with quantum entanglement, to tear spacetime asunder.

Tearing Spacetime to Pieces

Drumroll please… we are finally getting to the big new idea taking the physics world—and my heart—by storm.

In 2009, the physicist Mark Van Raamsdonk was thinking about the AdS/CFT correspondence, and about some recent papers that had been published relating AdS/CFT to entanglement. It turned out you could construct some interesting models of spacetime by leveraging the weird properties of entanglement.

For our purposes we will think of AdS/CFT as happening on a sphere. The 3D space is the inside of the sphere and the 2D space is the surface (or boundary) of the sphere.

Below you’ll see a slick rendering of this, which I’ve pulled right from an amazing Nature article on this issue.

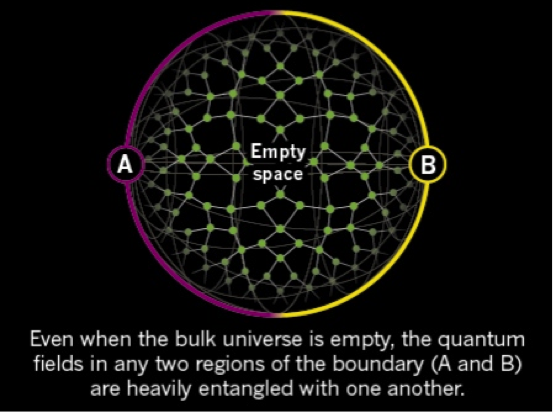
A and B are two regions of the outside surface of the sphere (the 2D boundary) and inside the sphere is empty 3D space.

Because the systems under consideration are quantum in nature, there will be some degree of entanglement between particles. Specifically, if we consider some particles on the surface of our sphere, those particles will be entangled with one another. (I don’t want to take us on a technical digression, but in the quantum theory used in AdS/CFT, even “empty space” some random “particles” flitting about.)

Van Raamsdonk was starting a sabbatical and decided to ask the following question: What happens if you get rid of the entanglement between particles in the 2D space (i.e., particles on the surface of the sphere)?

First, he considered a simple situation. Divide the 2D space into two halves. In the image above those two halves are the purple (A) and yellow (B) halves of the outer boundary.

Van Raamsdonk then figured out a way to “turn down” the entanglement between particles in the two halves. He accomplished this by monkeying around with some mathematical terms in the equations.

I’ll give a high level summary here of what he did.

Suppose we start at, say, a 10—which represents maximum entanglement. In this case we just get the sphere from above. Just boring old space.

But what if we turn down the entanglement between particles in the two halves of the boundary to say, a 6? What, according to the AdS/CFT correspondence, would happen to the 3D space?

Here’s what happens:

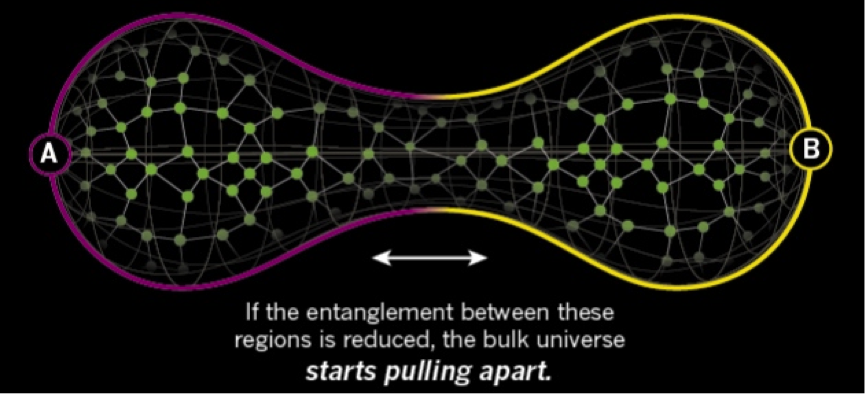
Umm, WTF?

It turns out when you turn down entanglement by some amount, the original space you started with starts to pinch off into two bulges, like a balloon being squeezed in the middle.

If we go all the way down to 0, this is what happens:

OH SHIT, THIS SEEMS BAD.

We. Literally. Just. Broke. Spacetime.

Apparent, as Van Raamsdonk found out, if you turn off entanglement completely between the two halves of the boundary, the interior space breaks into two separate pieces of space that are totally unconnected and might as well be parallel universes.

So what? you might be thinking. You just broke spacetime into two pieces. It’s weird, but what does it have to do with spacetime emerging from something else?

OK, now let’s imagine you split the original two halves of the 2D space into further halves. Any guess what happens? You get four completely separate pieces of space.

Now just keep doing that again and again until you have broken up space into a near infinite number of pieces, each of which has effectively no volume.

I don’t know what to call a near infinite number of disconnected pieces of space having zero size, but it’s damn well not a “space” that’s of any practical value.

On the other hand, you can imagine reversing the process by turning back up the entanglement between all those different regions of the 2D space. And lo and behold you could literally watch space emerge from that previously unidentifiable mess of spatial detritus.

If your jaw isn’t dropping right now—if watching physicists shred spacetime to pieces with a few tweaks to an equation, only to put it back together again, doesn’t knock your socks off—I don’t know what to tell you.

In Review

Of course we need the usual caveats: this is happening in mathematical spacetimes that are not like our universe. Also, I just showed you space being broken up and put back together, but not time, so that’s another issue to resolve. And, the thing that keeps bugging me even as my jaw is left hanging open is that we still had to start with a 2D space to generate the 3D space. So we magically created one of the spaces, but it required us to presume the existence of another space, which, so far as we know, isn’t itself emergent from something else.

Still, unlike the countless other wildly speculative ideas that have been thrown around about the nature of space and time over the last couple decades, I actually get the “gist” of this one. I don’t understand the math, but I don’t need to in order to appreciate the novelty.

After years of being underwhelmed by overhyped theories, I’ve finally found an idea that makes me do a double take. Maybe it’s completely wrong. Maybe AdS/CFT doesn’t tell us anything about how our actual spacetime works. Maybe it’s just a mathematical illusion.

Only time and experimentation can tell (assuming the former even exists).

But at least it’s not unoriginal, you know?