
Prompt Images
1. Black Holes are Really Weird
Black holes are really, really strange things. First, there is the whole “you can never escape once you enter one” thing—making them the Scientology of the astronomical universe. Even light, which literally sets the bar for how fast any other object in the universe can travel, can’t escape a black hole. I mean, that’s why they are called black holes, am I right?
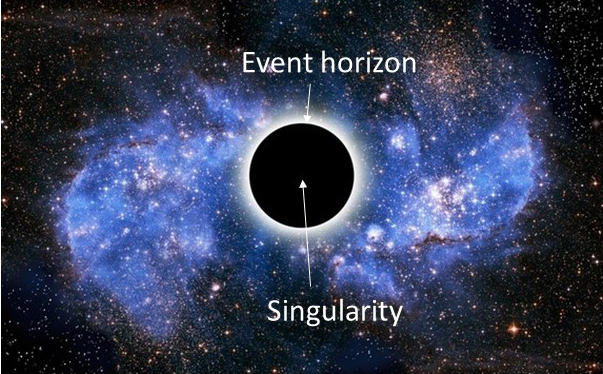
Anatomy of a Black Hole: The event horizon is the ‘boundary’ of the black hole—light (or anything else) that crosses that boundary can never escape. The singularity is just the place at the center of the black hole where all matter is crushed to an infinitesimally small bundle of energy—no biggie!
But black holes are actually even weirder than this. Consider this super high quality cartoon that I definitely did not make with a free online “create your own comic” tool. So here is the play by play: Joe and Jane are chilling outside of a black hole. Joe decides he wants to go explore the black hole so he makes a beeline for it.
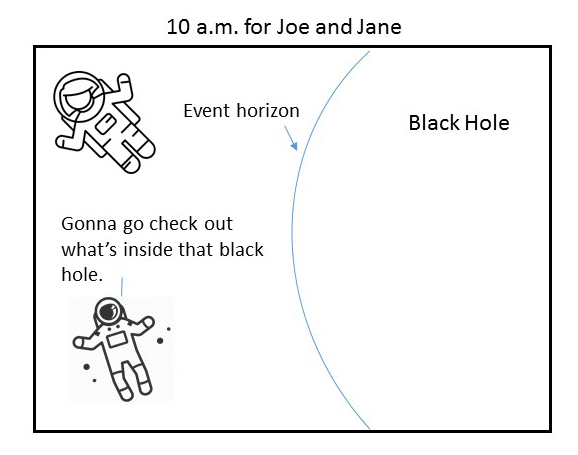
An hour or so later, according to Joe’s watch, he’s crossed the event horizon and now realizes he’s never getting out alive.
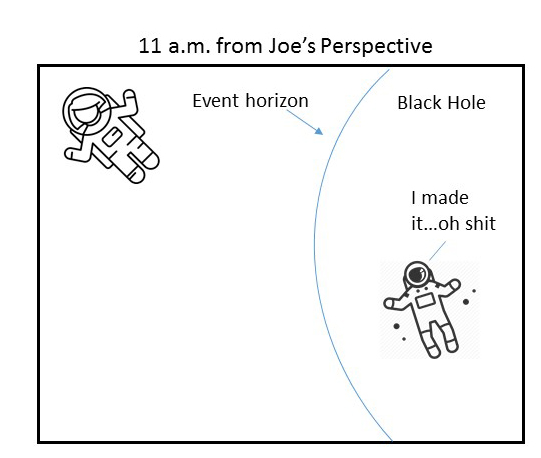
But, an hour later according to Jane’s watch, Joe is still making his way towards the black hole and has not cross the event horizon yet.

It actually gets weirder. The forces of gravity inside the black hole will eventually rip Joe to pieces, possibly later that same day depending on the size of the black hole. Meanwhile Jane will never, ever, see Joe actually fall in. Like ever. She could spend the last seventy years of her life watching Joe never quite fall into the black hole.
How is it that Joe can fall into a black hole and die in the course of a day, but Jane can live her whole life without ever seeing Joe fall in?
2. The Worst Analogy for Black Holes You Probably Have Heard
To understand how black holes work, we need an analogy that lets us bypass the math that physicists actually use to adjudicate the Joe vs. Jane paradox explained above.
The most common analogy for understanding gravity goes like this: spacetime is like a rubber sheet that is flexible. If you put a mass (i.e., the earth) on the sheet, the sheet will stretch out and create a pit into which other objects (moons, etc.) will fall in and orbit around. That “pit” is caused by the central mass is gravity.
Which, OK, is fine so far as it goes. But one fundamental problem with the analogy is that it invokes gravity to explain gravity. Gravity is the only reason that little mass would stay on the surface of the sheet in the first place!
And yet, the analogy works well enough just to explain the gist. Masses curve spacetime, and other masses change their motions in response to that new curvature in spacetime.
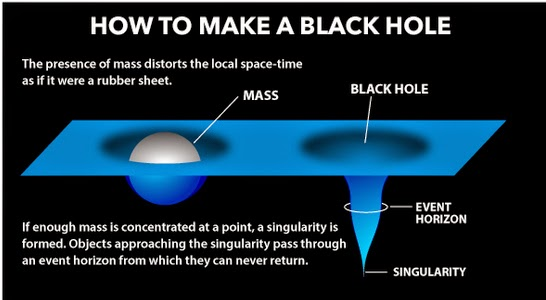
This analogy is OK, I guess. But we can and must do better!
But when it comes to black holes the rubber sheet analogy is just too crude to give you much insight. People start talking about that sheet being stretched down so much that the “curvature” of the sheet goes to infinity and this somehow explains why light beams that go beyond the event horizon can’t come out. So it’s like when Baby Jessica fell down that well, or…?
3. Dumb Holes to the Rescue
In The Black Hole War, Leonard Susskind describes an amazingly slick analogy for black holes, originally put forth by the physicist Bill Unruh. The “sonic black hole,” also called a “dumb hole,” analogy allows people to understand many of the strangest features of black holes without knowing how to solve this piece of 20th century hieroglyphics also known as “Einstein’s Equations:”
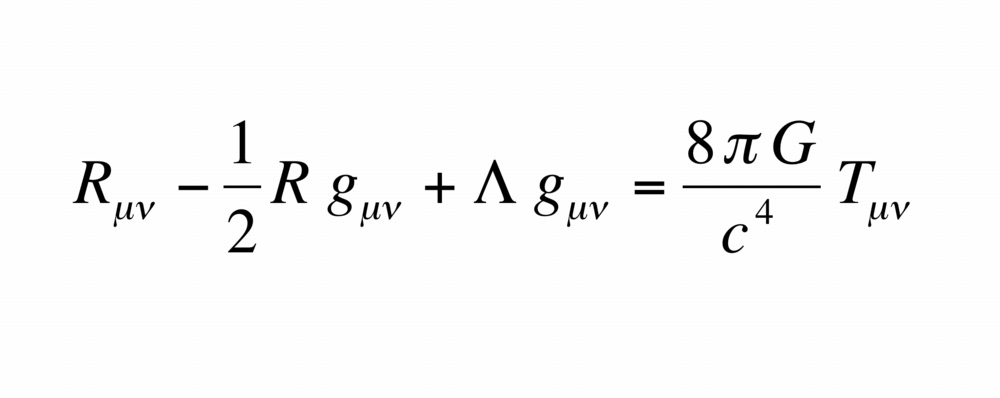
Here’s how Unruh’s dumb hole analogy works. First, forget about three or four dimensions. Let’s consider a really shallow lake, which is effectively two-dimensional. Put in some fish, who can hear but not see (we’ll see why this matters later). This lake is their “spacetime” by analogy. Now to make things interesting we add a whirlpool of sorts at some point in the lake and at the center of this whirlpool is a ball of spikes that would definitely impale and kill you on contact. Meaning: you do not want to get sucked into that whirlpool and dragged to the center.
Now it’s not just any kind of whirlpool, it’s a special whirlpool. At some distance from the center of the whirlpool (the exact distance doesn’t matter), the whirlpool spins faster than the speed of sound and presumably faster as you get closer to the center. This special distance is the “event horizon” of the whirlpool.
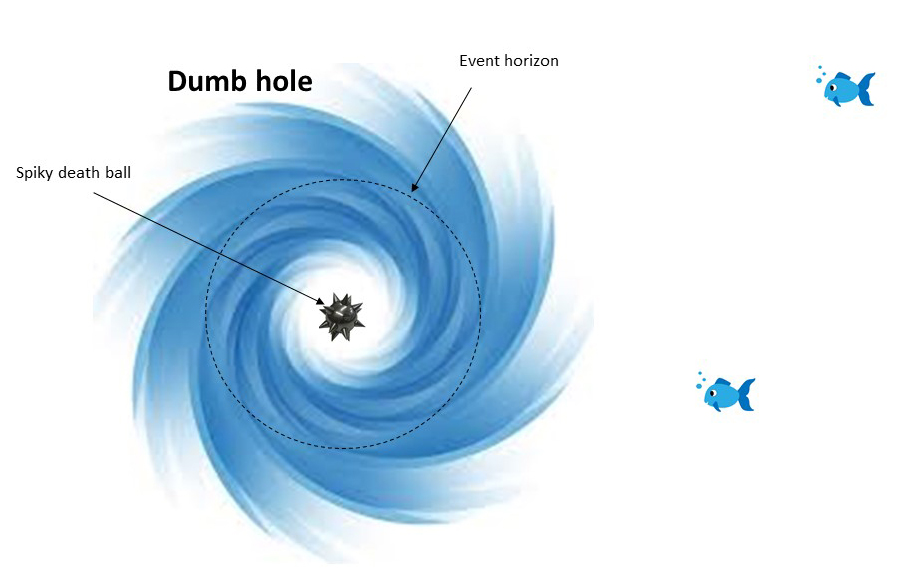
Anatomy of a Dumb Hole: The event horizon is the ‘boundary’ of the dumb hole—no sound (or fishes, who can’t swim faster than the speed of sound) emitted from inside that boundary can ever escape the dumb hole. The spiky death ball is analogous to the singularity of the black hole.
Quick sidebar on sound before we proceed: recall that sound travels at a fixed speed in a given medium (e.g., water or air). For example, the speed of sound in air is about 340 meters per second. Now if the medium is itself moving, that can change how long it takes for sound to travel between two places. It’s like walking on an escalator vs walking at the same speed on a staircase—it’s going to take less time on the escalator (or more time if you are moving in the wrong direction like an idiot).
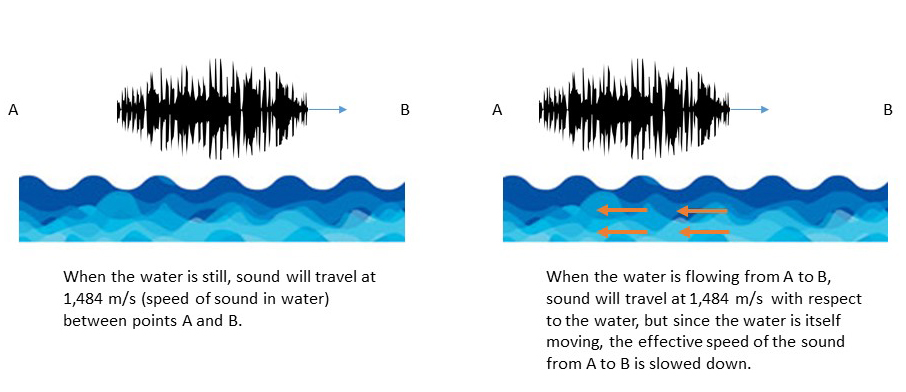
And now we return to our dumb hole. The bizarre whirlpool we described above is like a black hole in the following sense: any sounds emitted from inside the event horizon of the whirlpool can never escape, because the speed of the rushing water into the whirlpool is faster than the speed of the sound trying to escape from the whirlpool. It’s like walking slowly up a down escalator at Macy’s—you will never get to the Women’s Department on the second floor!
4. A Fish Called Wanda
In our lake, the fish—who are blind—communicate only through sound. So let’s say some fish named Wanda is swimming near the dumb hole. Imagine Wanda swims so close to the dumb hole that she passes that point where the water is moving faster than the speed of sound (AKA the event horizon). So Wanda is chilling inside the dumb hole and she tries to call out to her friend Franny. Except the speed of the water is such that her voice will never make it past the event horizon. Anyone swimming outside of the event horizon will never hear any sounds emerging from it. It’s complete silence.
Sound familiar? This is just like what happens with light in a black hole.
Now unlike the rubber sheet analogy, this dumb hole analogy allows us to explore the bizarre property of a black hole mentioned at the beginning of this piece. Namely, how one person outside the black hole and another person falling into the black hole can have two radically different experiences of “what happens.”
Imagine what happens as Wanda gets closer to the event horizon, before she’s fallen in. The closer she gets, the faster is the speed of the water towards the dumb hole. Suppose just before Wanda falls into the dumb hole she says, “Shit, I’m about to fall into this stupid dumb hole.”

Now just outside of the event horizon the water isn’t moving fast enough to keep her words from escaping. But, the water is still moving awfully fast—fast enough in fact to slow the speed of her words down to a virtual crawl. It’s going to take forever for sounds made by Wanda just outside of the event horizon to be heard by Franny who is far away. Hours, days, or maybe even years later, Franny will suddenly hear:

And the sound will be stretched out so much that Franny will never hear the end of the speech. Franny will actually die thinking Wanda is still near the boundary of the dumb hole, just doing that falling slowly into a dumb hole bit she loves so much.
Of course from Wanda’s perspective, she moves past the event horizon after just an hour of swimming. She doesn’t feel herself “slowing down” near the horizon. For Wanda, nothing really changes, except at some point she’s on a crash course with that super spiky thing at the center of the dumb hole which will kill her, no doubt.

5. Let There Be Light
Returning to our astronauts, the dumb hole analogy allows us to understand why Jane (who is outside the black hole) never actually sees Joe fall in: because Einstein taught us that gravity slows down light in much the same way that rushing water can slow down sound. In some sense you can think of space rushing into the black hole faster than light can escape from it. And any light that is lucky enough to escape the region just outside of the event horizon is drastically slowed down by gravity. From Jane’s perspective, it’s like watching a movie that keeps getting slower…and s l o w e r. . . a n d . . . .
OK, hopefully you sort of get why Joe and Jane disagree on what happens—but someone has to be right, right? Well, in the case of the dumb holes the answer is simpler: If Franny could see, not just hear, she’d be able to watch Wanda fall into the dumb hole long before she heard Wanda’s words. So the confusion about “what really happens” in that case is a bit artificial.
But with black holes it’s different. Nothing can travel faster than light, so there’s no way for Jane to ever actually know what happens to Joe apart from what she “sees,” or similarly, hears over a radio (radio waves travel at the speed of light too, so it’s the same issue). Now, Jane knows physics, so she knows from Joe’s perspective that he’ll just fall in and die. But she can never confirm that. There’s no way Joe and Jane can ever get together at a later time to agree exactly on what happened and when. They’ll never see “eye to eye” so to speak, in no small part because Joe will be dead.
In the end, black holes (and relativity, more generally) force us to answer the question “What really happened?” with the less than satisfying response, “Depends on who you ask, and what you mean by happened.”
In any case, it all makes sense now, right?
